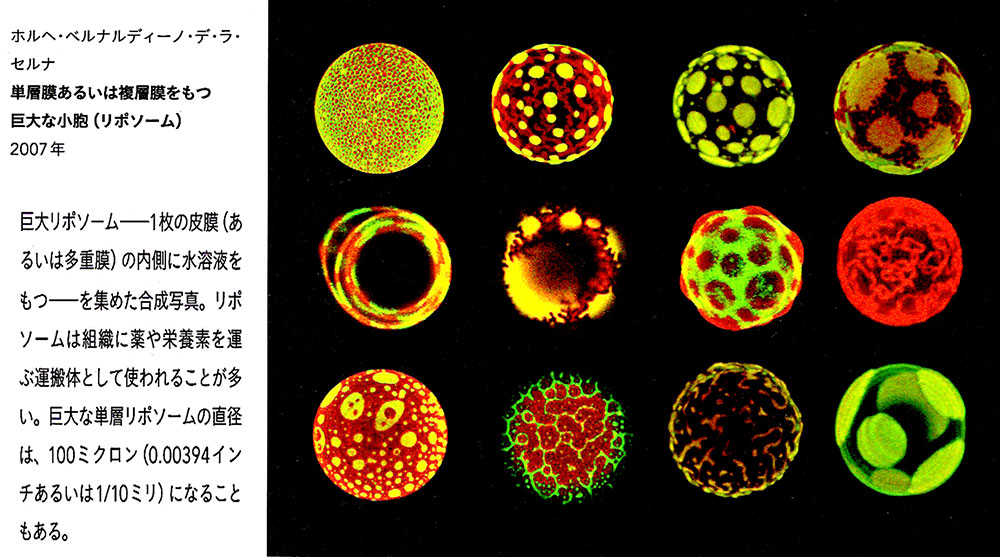
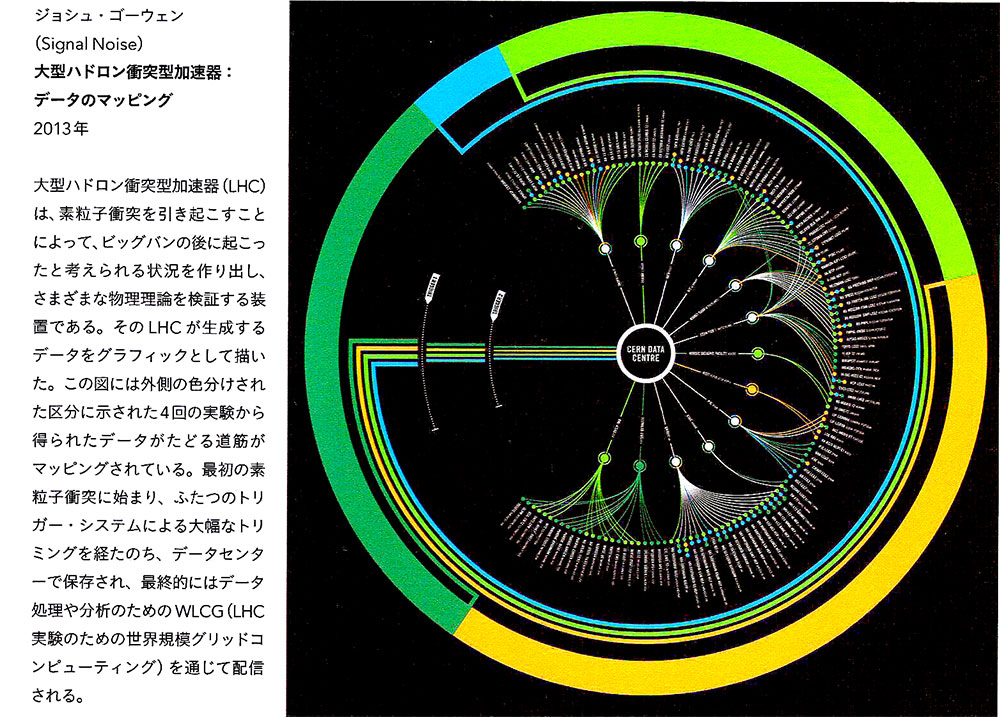
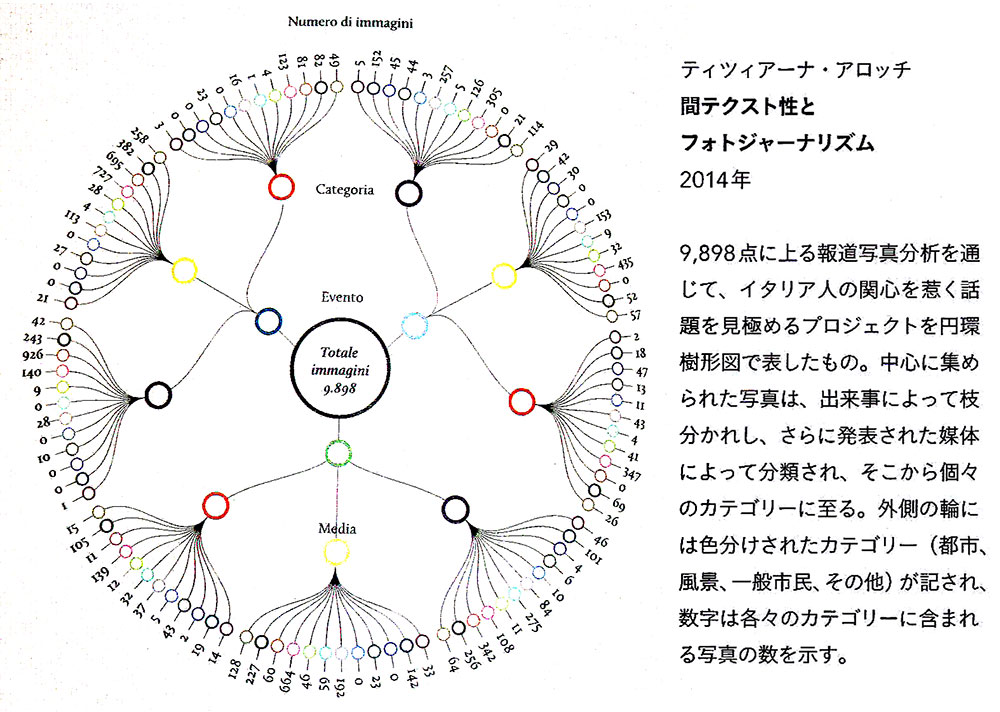
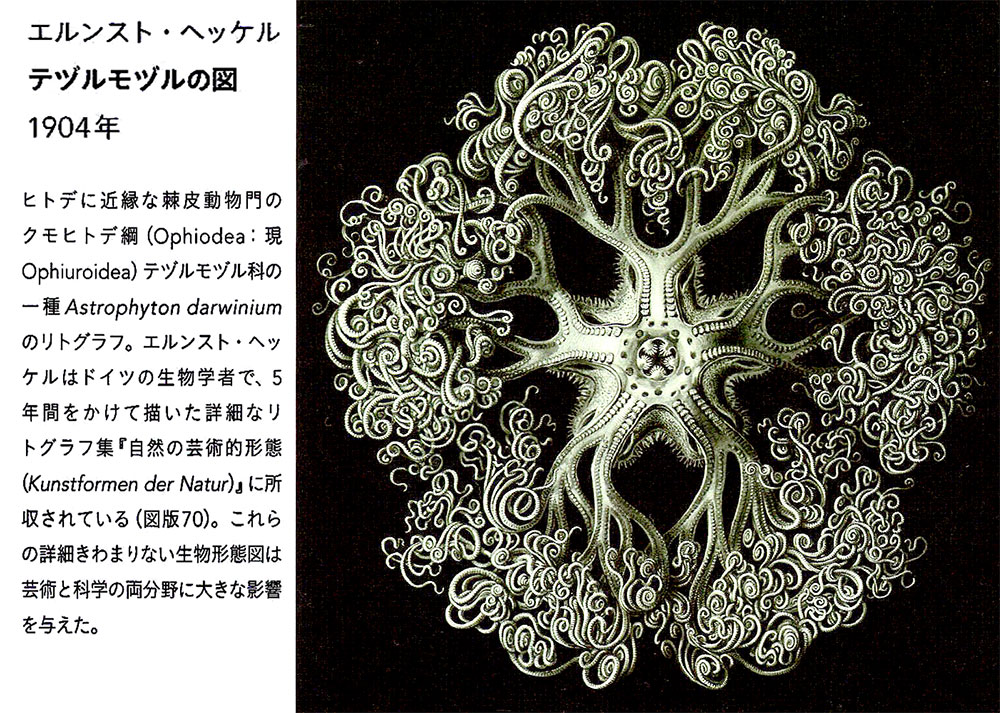
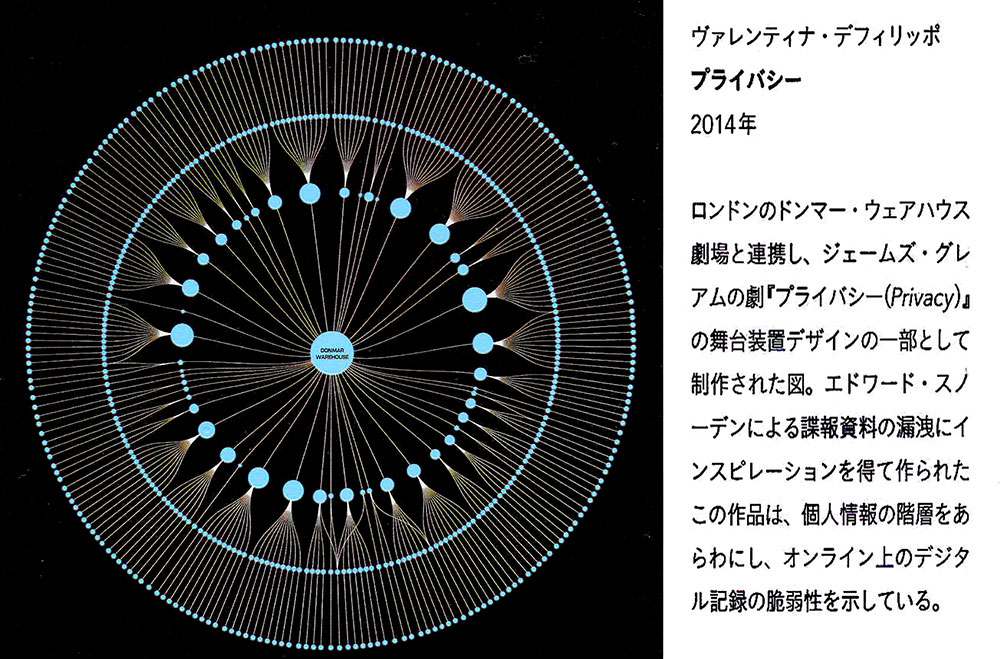
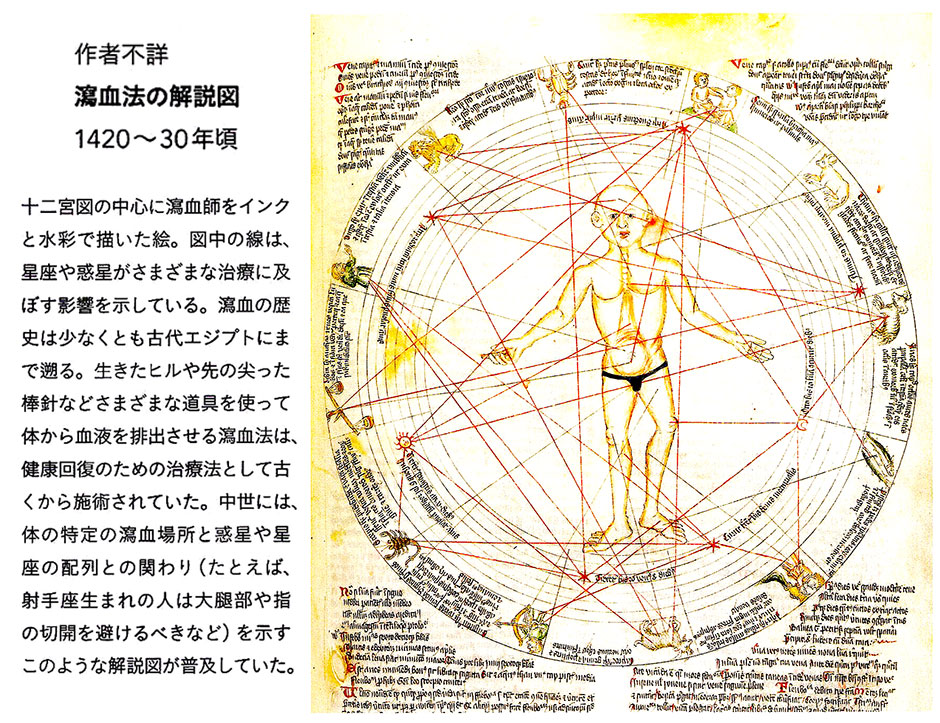
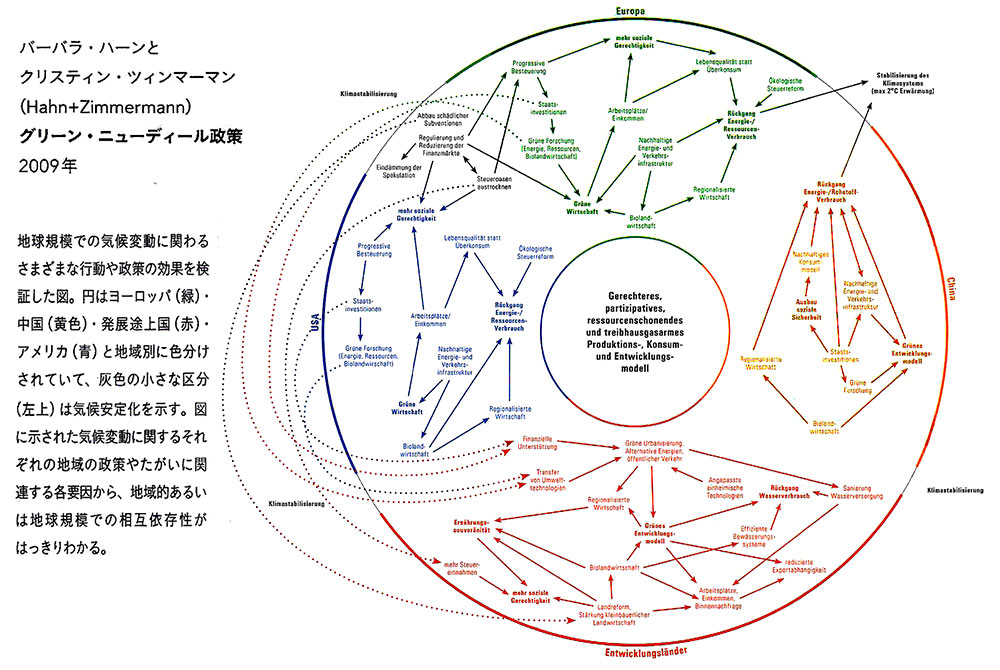
■円環の分類 A TAXONOMY OF CIRCLES
人間は分類する動物である。われわれは記載し、分類し、比較することによって現象を理解する。この慾望は自然科学の基盤であるばかりか、歴史・建築・文字・デザイン・芸術その他の文化的表現を理解する上で必須の手段でもある。図像の視覚構造を形式化しようという根強い努力のなかに分類という行為を垣間見ることができる。話はとても単純である。人間の言語がある決まった規則とメカニズムにしたがって並べられたブロックであるとしたら、図像も同じような論理にしたがうと考えられないだろうか？アメリカ人技師ウイラード・コープ・プリントンはこの衝動について自著『事実を示すためのグラフィック・メソッド』（1914年）で次のように説明している。
「英語の文法規則は複雑で数が多く、しかも規則と同じくらい例外もある。しかし、こんなに煩雑なのに、私たちは誰もがこれらの規則にしたがおうとする・・・そして、興味深いことだが、現在の音楽が楽譜という標準的な手法で書かれてどこの国でも演奏できるようになったのと同様に、グラフィック表現も国際的な言語となる可能性があるのだ」。
※ヴィジュアライゼーションのパイオニア、ウィラード・コープ・ブリントンが1939年に記した『Graphic Presentation』は、コンピューターが生まれる前の“データ視覚化ブーム”のきっかけともなった書籍である。やってくるであろう「データの時代」に備えるために、ブリントンは美しいインフォグラフィックをつくるためのテクニックを紹介している。
もちろん、このような遠大な目標を掲げたのはブリントンが最初ではない。中世盛期にまで遡れば、明らかに現代の情報可視化のルーツといえるきわめて強固な野心の発現である記憶術（ars memorativa）なる技法に行き着く。この記憶術とは、聖書の講釈のために利用された図像やダイアグラムであり、その効用は画期的だった。こうした記憶術の提唱者たちが作り上げた一連の原理は、秩序化・配置法・関連づけ・カテゴリー化など適切なレイアウトをどのように選ぶかに重点を置くもので、その多くは今日のグラフィックデザイナーや情報デザイナーにも受け継がれている。
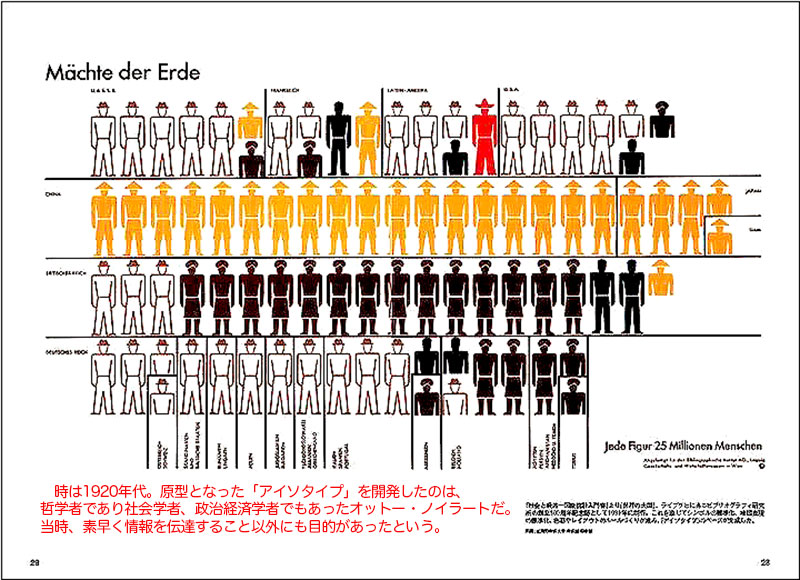
ルネサンス期に始まった知識を可視化しようとする気道は、やがて図像を視覚文法として再び体系化すべく考究の深化を促した。ドイツの碩学アタナシウス・キルヒャーやゴットフリート・ライプニッツ、スぺインの学者ライムンドゥス・ルルスら傑出した思想家たちが、画一化した言語学に取って代わる、あるいはそれをさらに高めるような、純粋で普遍的な記号言語をこぞって作り上げようとした。ここ2世紀の間にも、パウル・クレーやヴァシリー・カンディンスキーなどの画家が図像の基本構造を脱構築しようとする一方で、チャールズ・サンダース・パース、ルートヴィヒ・ヴィトゲンシュタイン、カール・ユング、ルドルフ・アルンハイム、ハンス・ヴァラッハ、リチャード・グレゴリー、セミール・ゼキなどの記号論者や心理学者たちもこの領域に乗りだし、一定の成功を収めている。さらにマックス・ビル、ブルーノ・ムナーリ、マイケル・トワイマンなどのデザイナーたちも、独自の方法で視覚リテラシーの限界を探ってきた。なかでも、1930年代にアイソタイプ（International System of Typographic Picture Education）の発展に最も大きく貢献したオーストリアの社会学者オットー・ノイラートのおかげで、今では世界中の建物や空港の至るところに視覚表示が使われるようになった。
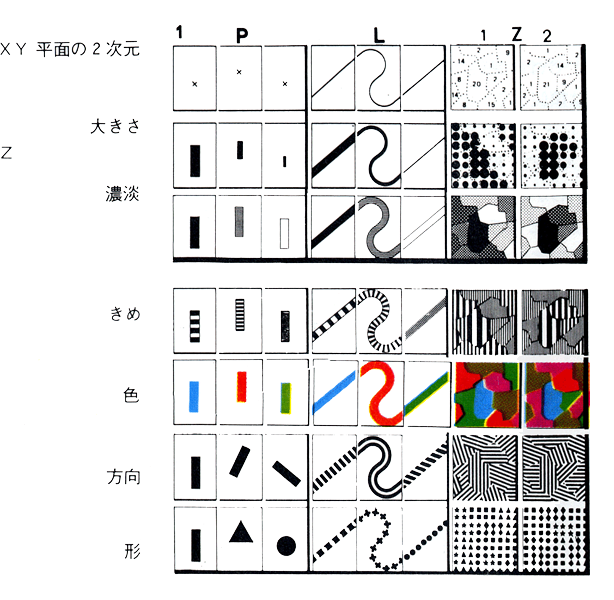
視覚言語の分析においてきわめて影響力のある成果として挙げられるのは、ドニス・A・ドンディスの有名な『形は語る：視覚言語の構造と分析（A Primer of Visual Literacy）』（1973年）である。ドンディスはバランスや対称性、対比など、視覚表現のさまざまな性質を小さな構成ブロック・・・点、線、色、形、方向、質感、大きさ、面積、動き・・・に分解し、それを「視覚力の骨格」と呼んだ。ドンディスによると、これらの構成要素には「あらゆる視覚情報の原材料が選ばれて組み合わされ」、デザインされるものの性質に応じて利用される一これが作品の最終目標である。
このような歴史的経緯を経て、現代の情報可視化の分野では、多くの研究者たちがグラフィックスの完全な文法を網羅する体系的な枠組みを構築しようとしてきた。フランスの地図学者ジャック・ベルクンは、著書『グラフィックスの記号学』（1967年）で、地図とグラフのための普遍的な枠組みの構築を目標に据えたが、これは今日でもこの分野の理論的基盤とされている。ロバート・L・ハリス（1996年）、エド・H・チ（2002年）、リーランド・ウィルキンソン（2005年）、ケイティ・ベルナー（2014年）もまた同じ方向を目指している。
長年にわたってこうした試みが積み上げられてきたにもかかわらず、視覚コミュニケーションの形式を包括的かつ統一的に体系化する方法は、少なくとも文字テクストほどにほ認知されていない。理由は単純だ。歴史学を専門とするデビッド・J・ステイリー教授が言うように、「書き言葉のシンタックスは直線的で一次元的である……」のに対し、「可視化のシンタックスはもっと制約がゆるく・・・…書き言葉のシンタックスよりもはるかに複雑なのだ」。書き言葉と可視化はどちらも情報をコード暗号化（encoding）して保存する手段だが、視覚的図像がもつ複雑な多次元性は、図像からのコード解除化（decoding）をはるかに困難にする。
視覚言語の包括的枠組みを構築することはすぐには無理であるとしても、対象を狭めて識別しやすいカテゴリーの原型を解明するという目標であればはるかに達成しやすいのではないだろうか。本書ではこの目標への第一歩として、昔から使われてきた最も普遍的な視覚的隠喩のひとつ・・・円環・・・の様態に焦点を当てる。
本書の例の大半は、情報可視化の分野から取られている。しかし、円環の包括的分類を目指すのであれば、考察対象となる範囲はある時代やある分野に限らず、もっと射程を広げる必要がある。歴史の深奥までのぞき込み、人間が成し遂げた革新を長いスぺクトラムで見直す姿勢が不可欠である。
※スぺクトラム・・・過去は繰り返し現在に再出現するからだ。私たちは高度な韻新ツールと新しいデータの山を手にしたにもかかわらず、歴史を通じて知識の伝達に用いられてきた視覚的隠喩に類似するときにはまったく同一のものをいまだに使っている。現代、たとえば2012年のプロジェクトが、15世紀の作品のすぐ隣に並べられているのはそのためだ。
注意深い読者にとっては驚くに当たらないだろうが、円環の普遍性はさまざまな分野にまたがっている。そこで、情報可視化分野からの数多くの例に加えて、芸術・生物学・建築・工学・天文学などの分野からもいろいろな例を取り上げた。一見するとまったく異質な分野と時代の事例が並んでいるのは、この本ならではの特徴であり、ひいては円環が融通無碍な適用対象をもつことの証しでもある。
円環を用いた試行錯誤の目くるめくばかりの多様性は、人間の発明の才を見事に示している。しかし、数々のダイアグラムや絵図を詳しく見てみると、大半の手法の背後にはごく少数のパラメーター群があることに気づく。
本書が提示する21のモデルは、それぞれの視覚的配置にもとづいて7つのファミリーに分類され、それぞれのファミリーは3つの原型から成る。最初の3つのファミリーには最も根源的な表現が含まれており、それらが円環体系の根幹にどれほど深く関わっているのかについて以下で強調しよう。
■ファミリー1 輪と螺旋 RINGS＆SPIRAL
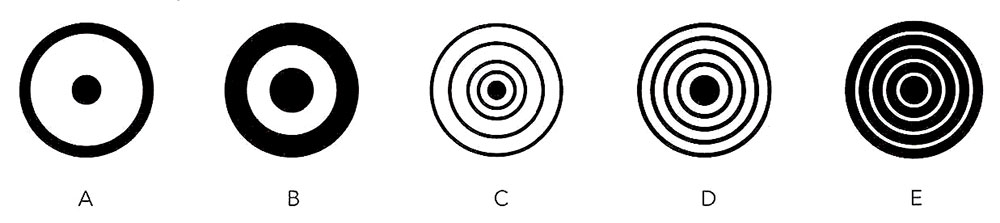
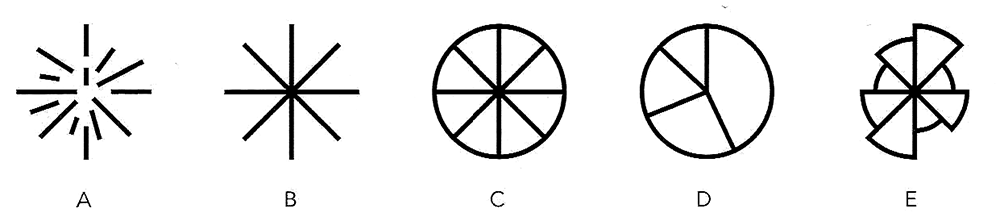
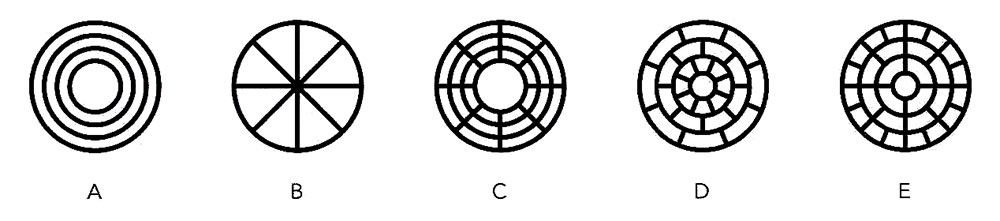
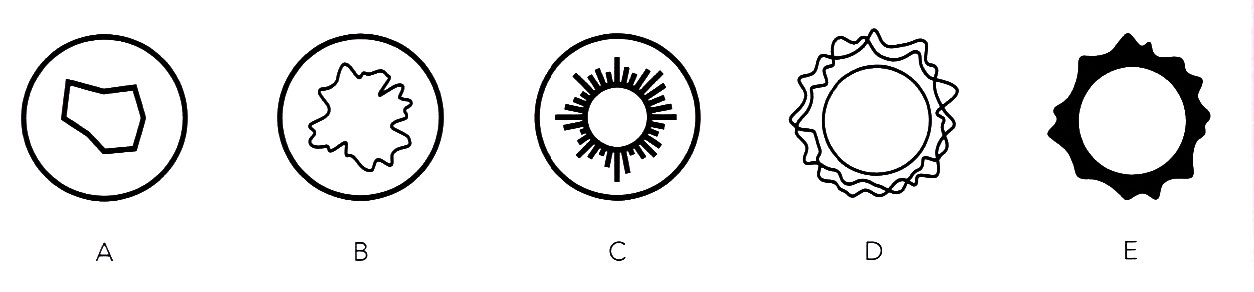
同心円のパターン。左から右に：（A）古代エジプトや初期の中国の筆記文字で使われた、太陽を表す天文的なシンボル：（B）イギリスやフランスなど多くの国の空軍が国籍を示すマークとして使っているラウンデルは、ロックバンドのザ・フーや小売業者ターゲットのロゴにも使われている；（C）ユタ州モアブのボタシュ・ロードにあるジャグ・ハンドル・アーチで発見された、紀元前2000年頃の岩面陰刻の模様；（D）スコットランド西部のアーガイル郡で見つかった、紀元前4000年頃の岩面陰刻のモチーフ；（E）アーチェリーの標的の典型的なデザインで、通常は（内側の輪から順に）黄色、赤、青、黒、白と色が塗られている。
序章で見たように、螺旋や同心円は人間が使った最古のモチーフであり、世界中の先史時代の岩面陰刻や岩壁画に見られる。(AとC）。螺旋は子どもが最初に描く形のひとつであると同時に、貝殻や植物の成長パターン、ハリケーン、銀河の巨大構造に見られる自然の原初的暗号でもある。同心円は、年輪から水紋に至るまで、多くの自然物バターンの特徴であるだけでなく、強い知覚訴求力を兼ね備えてもいる。螺旋と同心円はどちらも視覚刺激源として催眠術に広く使われてきた。これらの同心円や螺旋を動かすことによって催眠効果が高められるのは、これらの図形が少なくとも焦点をしぼり集中を促す作用があることの裏づけである。したがって、ダーツやアーチェリー、あるいは射撃などのスホーツで標的に同心円の模様が描かれているのは偶然ではない。(E）。類似のモチーフは、紋章や軍用品そして大衆文化・・・イギリスのロックバンドであるザ・フーから小売業者のターゲットのロゴに至るまで・・・でも広く用いられてきた。(B）。ラウンデル「円を基調としたシンボルやロゴ］は、イギリス、フランス、エルサルバドル、インド、トルコ、バーレーン、ガボン、ナイジェリアなどの国々の軍用機に付けられる重要な国章である。このファミリー1に含まれるその他の原型は、同心円のモデルを巧妙に現代風に変更したものである。それぞれの輪は、多くの場合、特定のデータ値に対応して長さが変わる。読み手側が個々の輪の長さの微妙な違いを読み取らなければならないため、このモデルには可読性の点で大きな問題がある。しかし、ここ10年で人気が高まり、携帯電話のデジタル・インタフェースから印刷されたチャートまで、さまざまな場面で使われている。
■事例作品
■ファミリー2 車輪図とパイチャート WHEELS ＆ PIES
スポーク（軸）を使ったパターンのいくつかの例。左から右に：（A）高速で移動しているときの視野を示す動線；（B）前進している印象を表すパターンの模式図。中心の消失点に向かう直線群として表されるこ（C）典型的な車輪モデルは、時空を超えて多くの文化で苦から使われてきたシンボルである。太陽十字（sun cross）としても知られる：（D）典型的な円グラフ（パイチャート）は、角度と面積に比例してそれぞれの区分にある数を割り当てる：（E）このパイチャートの変種は鶏頭図（p0lar area diagram）として知られる。各区分の角度は同じだが、中心からの長さが変わる。
マーク・チャンギージーは著書『ひとの目、驚異の進化：4つの凄い視覚能力があるわけで、私たちが原始時代から車輪というシンボルに魅せられてきた理由を説明するひとつの仮説を提示している。
※Mark Changiziは、 視覚 的錯覚を理解するための「現在の認識」仮説、文章、音声および音楽の起源に関する「自然を利用する」理論など、生物学的および認知的デザインの進化論的起源に関する研究を行う理論的認知科学者です 。霊長類の赤 – 緑の視覚の起源に対する皮膚シグナル伝達仮説、およびプルーニーの指に対するレイントレッド仮説。
チャンギージーは、最も古典的な錯視図に放射状の「スポークのような」線があるのは（A）それを見た私たちの脳が「これらの線は前進したときの動線だと解釈するからだ」と説明している。ファミリー2に含まれる円環の例の多くは、この抽象的なパターン、とりわけ消失点に向かって収束する数本の線で定義される最初のモデルから発展したものである（B）。透視図、ハイウェイを運転しているときに木や道が中央で収束するように見える錯覚、さらには映画『スター・トレック』で知られるようになった、ワープスピードで航行する宇宙船のSFの演出など、前進を感じさせる同様の錯視現象の例はいくらでも思いつくはずだ。収束する放射状の線を用いた絵や図は、美術にも科学にも数多く見られるが、その魅力は、ホタテの貝殻やヤシの葉から、放射状に光を発する太陽に至るまで、自然界に遍在するパターンであることに加え、このような錯覚を引き起こす力からも生じるのだろう。イギリスの画家ウォルター・クレインは次のように述べている。「画家が知覚し、表現することによって、作品のデザインに独自の生命力を与える原理をひとつだけ挙げるとすれば、それはこの放射線の原理だ」。
このファミリーの2番目(C）と3番目(D）のモデルは、この原初的な視覚モチーフを円で囲むことによって、新しいグラフィックの可能性を広げている。現代の円グラフ（バイ・チャート）は、1801年にスコットランドの技師ウイリアム・プレイフェアが考案したとされ、今では全体のなかの割合を表す基本的な可視化モデルとなっている。円の分割という概念は、青銅器時代のヨーロッパにまで遡り、車輪の概念に深く根づいている。なかでも最も有名なのが太陽を表す天文学的シンボルで、太陽十字、太陽車輪、あるいは年の歯車としても知られている。このシンボルは赤道と子午線で区分けされた地球、あるいは1年の四季を表す。太陽十字の円を4つではなく8つに等分するように変更すると、季節の中間点を表すことができる。8本のスポークをもつ、同様のモチーフにもとづくアイコンのもうひとつの重要な例が、法輪としても知られるダルマチャクラである。
このシンボルはヒンドゥー教徒や仏教徒の崇拝の対象であり、チベット仏教で頻繁に用いられている。弾けた円グラフのように見える最後のモデル（E）は、一般的にはローズチャート（rose chart）あるいほ鶏頭図（polarareadiagram）として知られているが、イギリスの社会改革者フローレンス・ナイティングールが有名な「東部での軍隊における死亡原因の図（Diagram of he Causes of Mortalityin the Armyin the East）」（1858年）で用いたことから広まった。
■事例作品
■ファミリー3 グリッドと経緯線網 GRIDS ＆ GRATICULES
ファミリー3の原型に属する円環の進化の系列。（A）の同心円を重ねた図と（B）の車輪モデルから（C）の静的な経緯線網、（D）のポルベル（車輪図）、（E）の日輪型などさまざまなデザインの可能性が生まれる。同様に、これらのグリッドの変形が、ファミリー4〜7で示す多くの視覚モデルの基盤となっている。
3番目のグループの円環は、ふたつの根源的な円環原型一同心円型（A）と分割円型(B）が組み合わさっている。このふたつの原型は、単独でも多数の変異を生み出すことができ、輪と分割の個数、一般には中心から周辺あるいは時計回りの順番、そして幅や角度の大きさによって可能性はいくらでも広がる。しかし、車輪の輪を増やすことにより、グリッドのもつ多面的な力はさらに拡大する。これほど柔軟なグリッドのもつ力は中世初期のデザイナーによって見いだされ、今日でも多くの円環図を支える礎石となっている。
このファミリーの最初のモデル（C）は制約がやや強く、内側と外側あるいは回転軸のどちらの方法を使っても、単一の線形的な情報パターンしか表せない。その大きな理由は図のなかでのそれぞれの輪の位置が同定されているためである。しかし、2番目のモデル（D）では、中心を軸にそれぞれの輪が独立して回転できるため、輪と輪の間で無数の組み合わせが生まれる。この柔軟性を生かした重要な道具が、先に紹介したボルベルという紙製の車輪図である。回転輪の組み合わせを利用したこの装置は、計算機の原型とされるほど驚異的なツールだった。
※ボルベル靴屋の息子であったペトルス・アピアヌスは、ドイツの著名な天文学者でした。この美しく作られた本は彼の最も有名な作品で、ボルベルと呼ばれる、惑星の動きを模倣する回転盤が組み込まれています。このボルベルは、月の黄緯を知る方法を示しています。中央には竜がいて、12 星座を差すように回ります。ボルベルは星占いにも使用されます。
このファミリーの3番目のグループ（E）は、入れ子状になった輪の放射状の区分を使って、階層構造を描く。日輪型、放射ツリーマップ、ファンチャート、入れ子円グラフ（入れ子パイチャート）など、さまざまな名前で呼ばれるこのモデルは、放射状に枝を延ばす木が具現する階層的論理にしたがって、図の中心を根とし、他の階層（輪）は内側から外側へと広がる。それぞれのセルは特定の数量やデータ属性に対応して変化し、色をつけることによってさらに別の特徴を付加することもできる。序列づけは、同線に向かう同心円の中心からの距離および親セグメントによって角度が決められた下位セクションでの位置というふたつの方法によって示される。
■事例作品
■事例作品
■ファミリー4 環状増減図 EBBS ＆ FLOWS
放射状の増減図のパターンを表すのによく用いられる環状増減図のパターン。左から右に;（A）単純化した放射図の概形で、パラメーターは少ない；（B）より複雑で多くのパラメーターをもつ放射図；（C）円形棒グラフて、人間の虹彩を連想させる；（D）放射状の多重線グラフ；（E）放射状の面グラフ。
4番目のファミリーには現代にも通用する多くの視覚モデルが含まれ、数量の可視化がさらに重視されている。このファミリーのプロジェクトのほとんどは、従来の棒グラフや面グラフあるいは線グラフでも簡単に表せるが、円環配置を使うことで、特に内側（中心に近い位置）から外側（周辺に近い位置）への動きによって、ある測定項目の増減を表現することができる。このため、横軸に比べると縦軸の数値が読み取りにくいという欠点はあるが、円形のモチーフに共通する訴求力をうまく引き出したものとなっているこ 人間の虹彩や放射光を発する太陽、そして花芯に見られる自然のバターンを無意識に想起させる鶏頭図・放射図・出生占星図などのダイアグラムには、従来の作図法に則ったものもあるが、特定の意味や関連件を強調する描き方を採用するものもある。
■事例作品
■ファミリー5 形状と輪郭 SHAPES ＆ BOUNDARIES
多用される形状と輪郭のモデル。左から右に：（A）円形の輪郭のなかにさまぎまな大きさの円を配置したもの；（B）円状の容器の内部空間を最大限に使うために円を最密パッキングした典型的なパターン；（C）いくつかの階層レベルを表す円環ツリーマップ：（D）自然界によく見られる単純なヴォロノイ分割図で、データ量を表すのに使われる；（F）3つの階層レベルを示すヴォロノイ・ツリーマップ。
※ボロノイ図は、ある距離空間上の任意の位置に配置された複数個の点に対して、同一距離空間上の他の点がどの母点に近いかによって領域分けされた図のことである。特に二次元ユークリッド平面の場合、領域の境界線は、各々の母点の二等分線の一部になる
ファミリー5の最初のふたつのモデルは、円のなかの円という注目されやすい図像の原型である。最初の例（A）では、複雑な関係を理解するためのたとえとして星の配置や運行を連想させる輪郭の内側に置かれた小円の大きさと位置によってデータ点の範囲を示し、円環ダイアグラムのもつ多変量データの表現可能性をわかりやすく表現している。2番目の原型（B）は円内最密パッキングという手法を使っている。これは特定の幾何学図形（ここでは円形の容器）の内部に構成単位である円を隣り合う円と重ならずに接するように配置する2次元的な技法である。さらに一歩進んだ段階になると、階層体系にもとづいて内部の円をさらに細かい円に分割していく例もあり、これは円環ツリーマップとして知られる(C)。このファミリーの最後のモデルは、ひとつの円を複数の幾何学図形に細かく分割したヴォロノイ図である(DとE）。この魅力的な分割構造は自然界の至るところで見られ、ツリー情造のような序列を表現することもできる。ヴォロノイ図の区分の大きさや色はそれぞれ異なるデータ値と関連づけることが可能である
■事例作品
■ファミリー6 地図と計画図 MAPS ＆ BLUEPRINTS
地図や計画図のモチーフ例。左から右に：（A）模式的な建築設計見取り図；（B）紀元前16世紀頃（下図）のバビロニアの世界地図の概略。海に囲まれ、ユーフラテス川が横切り、アッシリアやデルなどの多くの地域（内側の小円）が描かれている；（C）円形都市図の簡単な概略；（D）中世の地域地図や世界地図の典型的な輪郭；（巨）特定の地域を小さな世界に見立てた図で、通常は球体の中心に描かれる。
序章で見たように、何千年もの間、円は地図を作図する際の枠として繰り返し使われ、その起源は紀元前6世紀にまで遡る。地図製作において円がなぜいつも利用されやすい形状であったのかを考えると、それは私たちが丸い地平線を境界とする球面の地上に暮らし、空を見上げれば多くの球形の天体に囲まれているためかもしれない。ファミリー6の視覚的原型には、模式図から設計図そして特定の地域のより複雑な詳細図まで、さまざまな地図製作の技法が使われている（上図）。このファミリーの最後のモデルは「小さな世界」的・・・球という非ユークリッド幾何学図形をうまく活用し、核となる要素を強調する一方で、それ以外の要素は周辺に追いやる・・・アプローチをはっきり打ち出したものである。このモデルを見ると、アントワーヌ・ド・サン＝テグジュぺリの「星の王子様（The little Prince）」を思い浮かべずにはいられない(E)。
※アントワーヌ・マリー・ジャン＝バティスト・ロジェ・ド・サン＝テグジュペリ（Antoine Marie Jean-Baptiste Roger, comte de Saint-Exupéry、1900年6月29日 – 1944年7月31日）は、フランスの作家、操縦士。郵便輸送のためのパイロットとして、欧州-南米間の飛行航路開拓などにも携わった。読者からは「サンテックス」の愛称で親しまれる。
■事例作品
■ファミリー7 ノードとリンク NODES ＆ LINKS
放射状の樹形図とネットワーク図。左から右に：（A）模式的な放射樹形図：（B）詳細な放射状の木のモチーフで、分類樹形図として使われることが多い；（C）放射収束モデル。すべてのノードが基準円の周上に配置される；（D）可視的ノードを部分的に結合するネットワークで、平面天球図がその典型例である：（E）ノードを緊密に結びつけるネットワーク・モチーフで、リンクがより強調される。
ファミリー7は、円環を用いて実体間のつながりを表現するダイアグラムである。ノード（点）とリンク（辺）から構成される従来のグラフは、円環以外にもさまざまな形式がある。私の以前の著作をひもといていただければわかるように、それらは何世紀にもわたって、驚くほど多様な視覚的配置を発展させてきた。しかし、円環はツリーやネットワークを図式化するための足場として広く使われてきた。第一の原型は、放射樹形図によってある階層を表す(AとB）。第二の原型は、あるネットワークのあらゆるノードを基準円の外周に沿って並べる(C）。このファミリーの最後に紹介する本書のコレクション全体のなかで最も複雑なモデルは新しい文化的・科学的ミームであるネットワークだ（DとE）。このネットワークは、私が最初の著書『ビジュアル・コンプレキシティ・情報パターンのマッピング（2011年）において「ネットワーキズム（networkism）」と名づけた現代的思潮の存在でもある。
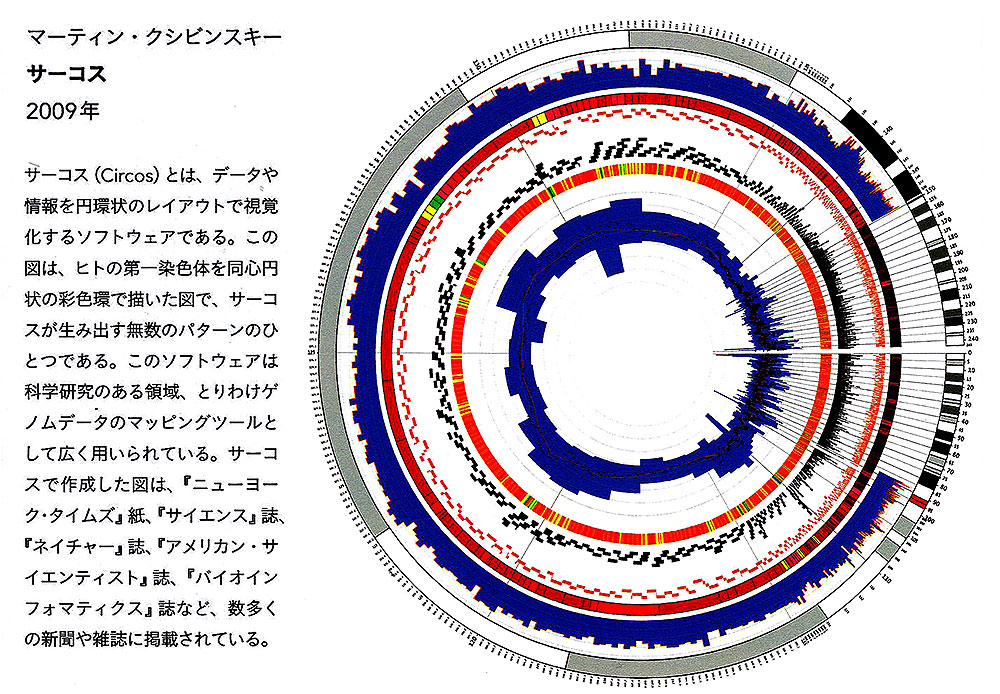
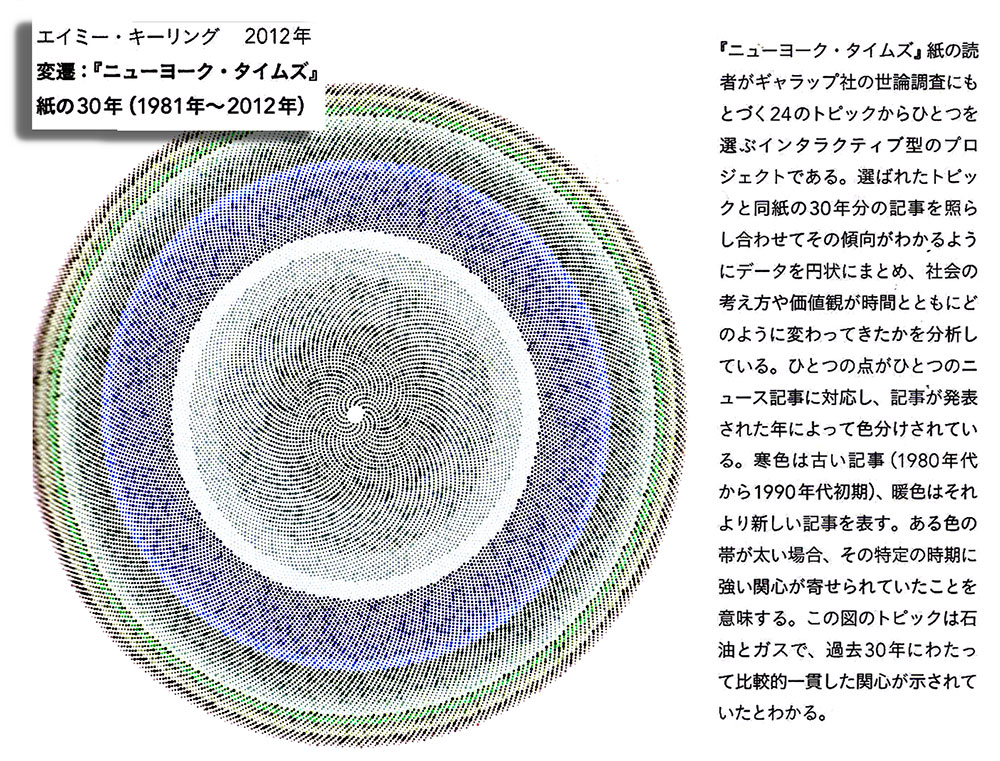
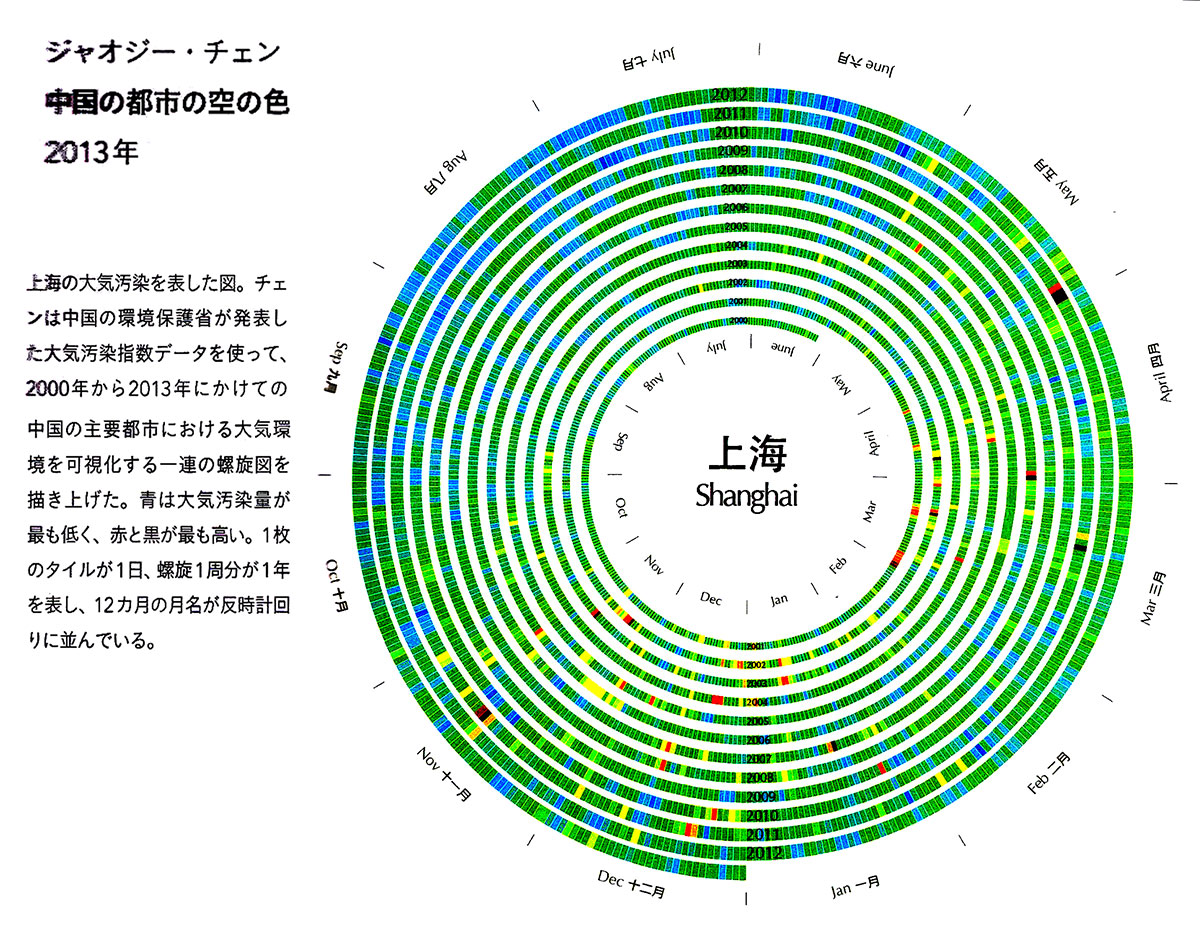
■事例作品
