構成的美術の諸相

■構成的美術の諸相

ウィリー・ロツラー

　人類は有史以前よりこの世界を美術という手段を通して解釈する際に幾何学的原理を用いてきた．幾何学が人間の基本的な体験であることをあらゆる文化遺産，あらゆる時代の美術が示している．単純な平面上の記号でさえ，メッセージの伝達手段としてだけでなく，自然を超えた力を支配し，超自然的霊力を表わす目的で使用された．太古の昔から深し、意味を込められたシンボルは，輝く太陽，渦巻，十字などのような単純な記号にと簡略化されてきた現代の交通，スポーツ，あるいは科学技術などの分野の多様な記号言語の中にも，幾何学の基本的なパターンが用いられ，コミュニケーションの役割を果している．

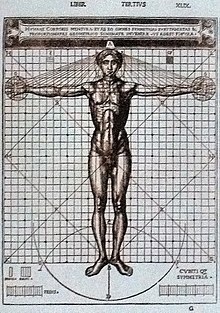
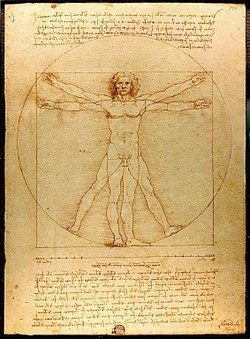
　線，面，立体，空間などの幾何学的構成や基本原色と副次色との明快な対比を用いて自然の法則を明らかにすることもできよう．「しかし，もしある芸術家が，幾何学を用いて自分の主張を証明し，根本的な真理を提示して見せるなら，世間は皆，彼の言うことを信ずるだろう・われわれは幾何学の中に閉じ込められているからだ．」と言ったのは，今日の構成的美術の作家ではなく，アルブレヒト・デューラーで，1528年に出版された『人体比例論』の中で述べていることである．

　幾何学的，構成的形体とは，あらゆる付随町主観的な要素を取り除いた形体，すなわち現実世界の複雑な現象とは無縁な形体であると考えてよい・このような純粋形体を明確に表現するには，基本的な平面と立体の形から始めて，円，正方形，正三角形，球，立方体，角錐，円錐，円筒などに考えいたればよい．平面，立体，空間やこれらを結ぶ函数は，ユークリッド幾何学の分野である．

　数学の一形式である幾何学と美術とは関わりがあるか，との問いに答えるには，古代ギリシア人がテクネー・techneという語によって，数学的法則とデザインや技芸のわざとを合わせた意味を表わしていたことを思い起せばよい。

　テクネーは，今日の意味でのテクニック（技術）を意味したばかりでなく，芸術も含めた工芸一般を広く意味していたのである．ギリシア人ほどの豊富な語彙力を持った国民でありながら芸術・ARTにあたる特別な語を持たず，応用水力学，建築デザイン，陶芸，壷絵，彫刻の各分野に対しテクネーの一語ですませていたのは偶然ではない。テクネーとは，自然の与える素材を用いて，思考と職人的あるいは技巧的技術を用いて人間のニーズに応える物を作り出す能力であると言えばこの語を最も点く定義できるのかもしれない．

　しかし，勿論われわれはここで，ギリシア人について論ずるつもりはないし，まして，レオン・バッティスタ・アルベルティやピエロ．テラ・フランチェスカ，レオナルド・ダ・ヴインチのように，自らを科学者と考え，数学者として仕事をし，かつ，数学の教本まで出したルネサンスの芸術家たちを取り上げようというのでもない．レオナルド・ダ・ヴインチなどは，ルネサンス期の最も重要な技術と数学の基礎文献であったフラ・ルカ・パッチョーリの『神的比例』（1509年）についての論文に数学に関する素描を描いたが，そのことが彼自身の権威をそこなうとは思っていなかった．これらイタリア人たちの数学研究の成果は，後にニュルンベルクのアルブレヒトデューラーによる1525年出版の実践幾何学の教本『コンパスと定規による測定に関する論考』，および，1528年，死後に出版された『人体比例論』に影響を与えた．

　このようなルネサンスの芸術家の美術の数学的基礎に対する情熱的であくなき探究心は，素描や論文に率直に表現されている．とは言え．それは，完成した美術作品の中では，主題となった画像のモチーフのかげに隠れてしまっており，わずかに構図の枠組や，物と空間との遠近法的処理にそれを窺い知ることができるに過ぎない。しかし、この「もっと幾何学を」という考え方は，人間と幾何学の潜在的な関係を表明しているものと考えられよう．

　幾何学的な要素は，未発達で本能的な形で、実際に先史時代の洞窟絵画にさえ見ることができる．すなわち、そこには有名な「自然主義的」な動物の絵と並んで水平．垂直，斜め，円といった線の体系が唐突にたびたび現われている．このように暗示的な幾何学的線を用いて・諸霊力，時間，性など，直接に描写することのできないなにかを象徴しようとしたのは疑いの余地がない．現代でもなお自然状態の中で生活しているスーダンのヌバ族のような種族が儀式の際行なうポチノ・ペインティングは，ほとんど幾何学的な文様に限られている．

　幾何学的デザインは，新石器時代と青銅器時代の農具に，何度も繰り返し現われ，地中海沿岸全域や中近東および極東の古代文化の初期幾何学様式へと受け継がれ，さらにプレ・コロンビア期のアメリカ大陸まで達し，ペルーのナスカの巨大な地上絵に続いている．

　このような幾何学的要素はよく誤って単なる装飾文様と見なされるが、主要文明の成熟につれて，なぜ，どの程度まで，人物や事物のだんだん本物に近くなってゆく自然主義的表現におされて，退化していったかはここであえて追求しない．重要なことは，各時代を通し，どの文化をとっても，霊力と数学の関係が，神的比例すなわち黄金分割におけるほどの完璧な調和を常に保っていたわけではないにしろ，宗教家や思想家，芸術家らは両者の関係を認めてきた点である．画像を忌み嫌うイスラム世界では数学者や哲学者の関心が美術に他の地域に見られない程深い痕跡を残した．懐疑心の薄い西洋人には，イスラム建築のレリーフや壁面装飾は一見すると混乱し無秩序に見えるため、単なるありきたりの飾りに過ぎないと思われ，複雑な線の構成や，数学的体系をもつフォルムなど，イスラム美術が，おそらくは最も深く数学の影響を受けた美術であると見抜〈ことは困難である．

　しかし，幾何学的デザインは瞑想への契機として，また，他の方法では見るここもできず言い表わすこともできない神性を表明するものとして利用されている。事実そのような意図のもとでしばしば利用されている。そしてこの点はイスラム美術だけでなく，ヒンズー教の中のタントラ美術や極東の美術にも幾分か認めることができる．日本の石庭に見られる禅の線的構造はその一例である．

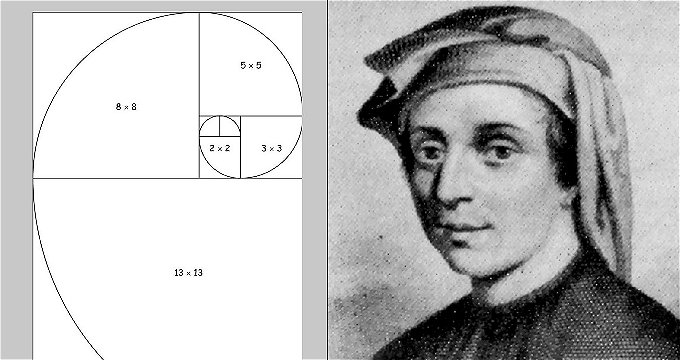
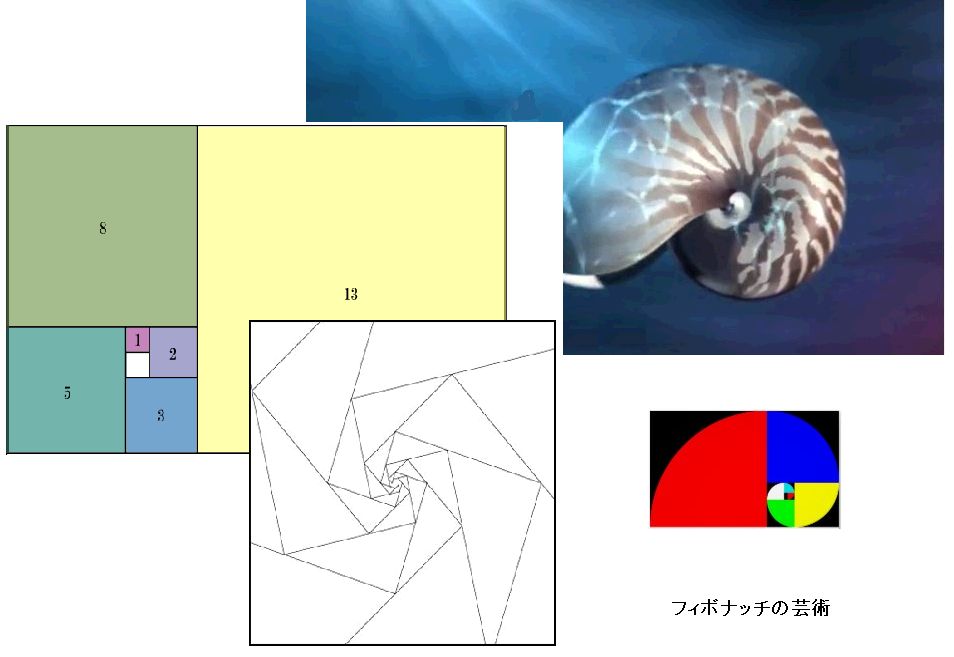
　しかし，超自然と数学との関係をあまり深く探求する必要はない．キリスト教から一例だけ挙げるとすれば，三位一体が真上に頂点を？与った正三角形で象徴されていることである．これと同じ源から中世の教会の平面図や側面図に頻繁に用いられている数値の複雑な比率も発している。級数と数列は，合理的なものから不合理なものへ，すなわち．理解し得るものから，認識し得ないものへの移行についての思考を常に人間に促すものであった．こうして，たとえば，中世の有数の数学者であるピサのレオナルド・フィボナッチは13世紀初頭に自分の名を冠した級数を展開したが，この級数は近来になってコンセプチュアル・アート，ミニマル・アートの代表的作家，特にマリオ・メルノやドナルド・ジャッドによって取り上げられ，美術の実制作の面で豊かな成果を挙げるものとなった．

　このことは美術において数学や幾何学が目新しいものでないことを意味するのだろうか．その筈はイエスでもあり，ノーでもある．今まてこ述べて来た世界美術の底流としての幾何学とは全く別個に，西洋美術を代表する者たちは常にあらゆる平面形体における幾何学的な基本法則，すべての空間形体における立体の基本法則に関心を持ち続けてきた．デューラーが「根本的な真理」と呼んだこの点は作品の主題の多様な外観のかげに隠されてきただけであった．われわれは現実の再製こ取り組んだ作家たちが幾何学を利用した例を美術史上数多く知っている．ジュネーヴの画家で，コローの弟子で、ホドラーの師であったパルテルミー・メンは，1850年以降，人体という有機的形体を，多面三体的な構成要素に分解して教え，ボール紙片を適当な角度で寄せ合仁せて構成した頭部を作り上げた．このような教育法は，キュビスムが現われる50年以上前のものであり，おそらくもっと古くからあったものであろうが，一方で1915年以後ナウム・ガボによって，さらに後にアントワーヌ・ぺヴスネルによって作られた房構造の頭部やトルソーに通じるものである．風景を単純な立体に分割して見せたセザンヌの見解もー般によく知られている．

　しかし初めて純粋形体の世界へ踏み入ることができたのは，近代美術が完全抽象　あるいは非対象へと急進的一歩を踏み出した時であった．20世紀美術の画期的業績の一つであるこの一歩が踏み出されたのは，1910年頃である．この業績に対する栄誉は普通ワシリー・カンディンスキーに与えられている．彼はまさに1910年，ミュンヘン滞在中に具象的なもの，もしくは外界の対象物を出発点としない最初の水彩画一最初の「純粋」または「絶対」絵画－を制作した．しかしまだ問題は漠然としていた。同じ問題が，時を同じくして，さまぎまな場所で，多くの芸術家たちの心を占めていた．可視世界の諸相を模写することを一切拒否した結果，作品の形式と内容との完全な一致という，当時ではセンセーショナルな現象にいたった．実際には線，面，色調，色彩や，造形，空間，質感などのデザインを制作するために作家が用いる手段がその付随的機能から，あらゆる場所で，一撃のもとに解放されたというわけではなく，徐々に段階を踏んで行なわれたのである．美術作品はもはや何かを「意味する」ものではなく，見えるがままのものとなった．作品は客観的世界すなわち外部のリアリティを参照し直すことなく，作品自体のリアリティと自立性が絶対のものとなった．

　このような目に見える現実の拒否は，1910年代初頭に二つの方向に分かれた・一つは，自由で表現力豊かで感情的な様式，もう一つは，厳密で整然として幾何学的，構成的かつ合理的な様式であった．若き日のカンディンスキーに見られるような感情的な表現形式は，フォーヴィスムと表現主義の延長であり，合理的表現形式の方は，キュビスムがさらに発展したものと理解することができる．表現主義的非対象は，シュルレアリスムの自動描法などいくつかの段階を経て，50年代の抽象表現主義，タシスム，アンフォルメルそしてアクション・ペインティングヘと続く．幾何学的非対象は，地域的な流派やグループの違いこそあれ，また，時と共にその傾向は変化したものの，最も広い意味での構成的美術と呼びうるものを生み出した．

　この展覧会には，それらが時と場所の点で大いにへだたった運動の産物であっても，一般的に「構成的美術」として分類されうる作品が集められている．この構成的美術には多くの概念や用語が摘み合っていて，この分野をよく観察しようとする者は，しばしば混乱するようである．しかも，これらの概念や用語は作家や批評家によって異なった意味合いで用いられることが多く，さらには各国語の違いによる用語の変化も混乱の一因となっている．

　「抽象」という語は狭義の字義通りの意味では，客観的ないしは具象的なモチーフを単純な基本的形体に簡素化する過程を言う．抽象の過程を経て出来上がった最終的な作品はもはや客観的現実の凝縮あるいは類型化であるとは認識しかねる幾何学的形体の寄せ集めとなる．初期の構成的作品の中には今述べたような過程で作られたものもある．今日でも程度の差こそあれこの幾何学的「抽象化」を個人で実践している画家や彫刻家が存在する．

　一方この抽象過程と正反対の方法をとる作家もいる．すなわち，外部から来るすべてのインスピレーションを拒絶し，作家自身のイマジネーションの中に生まれる非対象の幻想と観念に目に見える現実の形を与えようとする．構成的作品の圧倒的多数が，この第二の方法によって制作されてきた．しかし，「抽象」として分類され得る作品と，もはや「抽象」の過程をとらなくなった作品との境界線上に位置する作品もある．例えばカンディンスキーの1910年から12年，モンドリアンの1915年から17年の間の作品がそれである．

　数年のうちに，心に描かれたものを目に見える現実の形に翻訳するプロセスと，それと全く異なる「抽象」のプロセスとを明確に区別するために，「非具象non−figurative」，「非対象non−Objective」，「非再現的nonィepresentational」あるいは「絶対美術absoluteart」などというさまざまな用語が作られた．この間題に最も筋道の立った解答を見出したのはオランダのデ・ステイル運動の創始者の一人であるテオ・ファン‥ドゥースブルクであったことは間違いない．彼は1930年に「具体美術 concrete art」の観念を提唱している．ドゥースブルクによればこの種の美術の目的は抽象的あるいは想像上の画像に具体的な形体を与えることである．芸術作品をこのように「具体化」と捉える考え方はすぐにカンディンスキーやアルプなどに受け容れられ，繰り返し取り上げられた結果，1944年以降チューリヒのマックス・ビルにより次のようにさらに厳密に定義された．「具体化の目的は抽象的思考を，五感を通し現実のものとして理解しうるものとすることである．ここでいう『具体』とは「抽象』の反対語である．」

　構成的美術のさまざまな傾向をどう呼ぼうと，1910年から15年にかけて，ヨーロッパ諸国の作家たちは，初めのうちは個々に，後にはしばしば互いに独立したグループを形成して，平面と立体を規制する幾何学的法則にかかり切っていた．今日これらの先駆的作品を調べてみると，そこに，冒険と発見への情熱に駆り立てられ，しかも，進歩の重要性を意識していたある世代が勇敢に新天地へと前進して行く印象を受ける．作家たちの声明文などを読んでみるとこの印象は一層強い．この幾何学的構成的美術の造形法則は，何度も研究されているが，絵画的創造の基本そのものへの回帰と考えることができる．それは意識的で，暗に自由であり，時に体系的でもある形体と色彩の基本法則の研究であり，その効果に対する緻密な観察でもある・

　基本的なものに対するこのような関心は外見の紛らわしい多様さ，言うなれば現実世界の混沌を明快で理解可能な秩序と対決させようとする意志の表明とも思える．だからこの混沌を征服するためのヒントと助けをこれら秩序立った法則の中に見出そうとする試みへ，ほんの一歩だが踏み出したのである。そこで構成的美術は，様式とか美学上の分野にとどまらず観念的世界概念にまで結びつくことがある．構成的概念は，現実の世界と社会生活の変化に適用されるとユートピア的社会改良計画の性格を見せる．この事実はオランダのデ・ステイルの代表的作家たちや，ロシアのシュプレマティスムや構成主義の主唱者たちを見れば明らかである．理性と感情はすべての創造的努力の二つの対極的な源泉であると考えるなら，理性から出発した構成的美術は，結局，感情的もしくは，表現的な美術とは相容れないものであることが理解されるだろう．

　このような感情的なものと理性的なものの対照はすでに優美で有機的あるいは植物的な形体の世界が，規律正しい幾何学形体と出会う1900年頃のアール・ヌーヴオーの運動の中に感じ取ることができる．しかし構成的美術の本当の種子は間違いなくキュビスムと未来派の中にある．それは，両方とも可視現象の世界とのつながりを否定しなかったが，現実の分解と，新しい自律的な美術としてのリアリティの構成に関わっていたからである．ピカソとブラックによって創始されたキュビスムの運動は，風景画，人物画，静物画といったようなモデルとの密着を止め，対象の分析の段階において，さらには総合の段階においてはよりはっきりと線，面，立体などの要素へ戻り，遠近法を用いない新しい様式で新しい絵画的なリアリティを作り出すことができた．キュビスムは時の社会や生活への無関心を繰り返し宣言しているが，イタリアの未来派は，キュビスムの手法を借りながら近代都市生活のテンポとドラマを熱心に美術に近づけようとした．イタリアの未来派が公に掲げた目的は「運動」の要素，したがって「時間」の要素を美術に取り入れることだった．

　いずれのアプローチも構成的美術の発展には欠くことのできないものだった．1912年から14年のヨーロッパ美術の中で，未来＝立体主義Futuro−Cubism（ロシアの前衛派は当時自らを立体＝未来主義Cubo−Futurismと呼んでいた）と呼んでしかるべきこの流れは，まさに確固とした構成的美術の展開への序曲であった．

　その突破口が開かれたのは1915年前後であった．可視的現実の足蜘はついにふりほどかれ，マレーヴィッチが後に「非対象の世界」と呼ぶようになった「新しいリアリティ」が一貫して追求された．オランダとロシアで二つの作家グループが互いにまったく独自に絵画法則を発展させた．オランダでその基礎を築いたのは，ピ工ト・モンドリアンとテオ・ファン・ドゥースブルクであった．二人は共同で，時には同じ考えを持つ建築家や画家の支持を得ながら，1917年に彼らが創刊した雑誌アデ・ステイル三の名で知られるようになった美術理念の基礎を築い　スタイルた．「様式」を意味するこの名称が示すように，その目的は新様式を作り出すことであったが，その新様式とは美術だけに限定されたものではなく，環境全体を形成するための新しい統一的な処方を目指すものであった．建築はこの様式の中で極めて重要な役割を持ち，建築物の内外の空間的関係を包含する統一体として理解された．最終的にはデ・ステイルは新しい生活様式をも意味し，芸術はその尖兵として理解された，しかし，デ・ステイルの指導者たちは社会文化のユートピアを予告する革新的な理論を著わすと同時に依然として絵を描くことも止めなかった．モンドリアンは，自身の絵画概念である「新造形主義」に基づいた作品を作った．これに対して，当時完全に建築に没頭していたファン・ドゥースブルクは「要素主義（エレメンタリズム）」で応えた．モンドリアンが一部を原色で塗った水平と垂直の線のコンポジションで調和のある平衡を生んだのに対し，ファン‥ドゥースブルクは彼の直角の枠組を繰り返し傾けることによって彼の言う「カウンター・コンポジション」の対角線をつくり出し，これによって幾何学的構成的美術に生命体のダイナミズムを導入した．

　ロシアにおける状況はもっと複雑だった．というのは，そこでの芸術における激しい変動や革命は，1905年に不成功に終った政治革命の代償の役割をある程度果したからである．若い芸術家たちのグループが互いにしのぎを削り，対立し，凌駕し合いながら，キュビスムと未来派が与えた可能性のすべてをものすごいスピードで慌しく経験して通った．その行動には無政府主義的な要素やヨーロッパのダダイズムを予感させるショッキングな効果に対する喜びが見られ，作家の行動や作品によって社会を挑発しようとする態度があらわれていた．その結果が最初にはっきりと現われたのは1915年，マレーヴィッチが形（四角い背景の上に四角形または十字のみ）と色彩（言うなれば黒と白のコントラストにまで）の極端な還元と見なされる様式に到達した時であった．彼はこれを「シュプレマティスム（絶対主義）」と呼んだが，それは彼の作風が彼以前にあった美術より進歩していることを意味するよりは，芸術的感受性の至高性を意味するものであった・彼は「シュプレマティスムはすべての絵画を白いカンヴァスの上の黒い四角形に凝縮してしまう．私は何も発明してはいない．私は自分の中に夜を感じただけで，その中に私がシュプレマティスムと呼んだ新しいアプローチを見ただけだ．」と述べている．マレーヴイツチの大部の理論的著作を読むと，デザインの問題は確かに書かれているが，結局彼の関心は哲学上の問題だ，という印象を受ける．

　ロシアの他の構成的傾向の美術家たちはマレーヴィッチの作品のもつ不合理な要素や，宇宙とも完全な無ともとれる想像空間の前に置かれた基本線と平面形体の微妙なバランスを受け入れなかった．彼らの反感は十月革命後にさらに増大した．彼らにとって芸術家とは夢想家でも宗教家でもなく新世界の建設者であり，技術と工業によってのみかなえられる新しい要求をかかげた社会主義労働者国家の確立を支える理念を提供するはずの着であった．これらの作家たちは楽観的にも自らを「構成主義者」と呼んだ．アレクサンドル・ロトチエンコはそのひとりであったが，「新しい人間」の原型は間違いなくエル・リシツキーである．彼は自身の美術作品とデザイナーかつジャーナリストとしての多彩な活動を通して，この仮説的人間像を明瞭に訴えた．ソビエト国家は，当初これらの構成主義者を国の大義の支持者として歓迎したが，結局は彼らを必要としなかった．スターリン時代となって「社会主義リアリズム」宣言の中では，構成主義は形式主義であり，危険分子であるという非難さえ受けるにいたった．

　1920年代には構成的美術の国際化現象が見られた．その主要な舞台はドイツで，中心地は当時活発な活動の場であったベルリンであった．ロシア展とすでに西ヨーロッパに移住していたロシア人作家たちによって，東ヨーロッパの構成主義の成果が持ち込まれた．ドイツ国内ではまずワイマールでそして後にデッサウにおいてバウハウスがその推進力となった．この画期的な学校はこれまでの美術学校とは異なって，進歩的精神で活気づいており，新しい基礎デザイン課程を通して構成的美術を奨励した．さらに有意義だったのは，パウル・クレー，オスカー・シュレンマー，ヨハネス・イッテン，リオネル・ファイニンガー，ワシリー・カンディンスキー，ラーズロ・モホリ＝ナジ，ジョーゼフ・アルバースらをはじめとする作家たちが一諸にあるいは次々にバウハウスにおいて活躍し，特に作品を通し多大の貢献をなしたことである．ワイマール共和国時代のドイツは新たな独自性を模索中であり，1922年にはデュッセルドルフ会議で「進歩的芸術家の国際団体」の結成が試みられた．オランダのデ・ステイルとロシアの構成主義の代表者が一堂に会したのもこの会議であったことを思えば，両グループにとっても一つの驚きであったろう．以後，雑誌，旅行，展覧会を通じて国際交流が活発に行なわれ，これらの接触に刺戟されてまもなくヨーロッパのほとんどの国で，構成的美術を制作する画家や彫刻家，またその団体が見かけられるようになった．

　構成的原理は今や世界的規模で行なわれる美術理念交換の媒体となった．国ごとの特色と個々の様式の差はあったものの概略では以下のような根本的一致があった．すなわち，美術というものが，その孤立の中から脱け出なければならないものであること，また，すべての進歩的勢力の統合，すなわち，建築や都市計画，工業デザイン，タイポグラフィや写真，環境の整備とヒューマニゼーション，演劇，映画などの統合が芸術と現実の生活の橋わたしをするものであることの二点だが，中でも美術自身がこの役割を果すべきであると考えられた．この運動のバイオニアたちは単に「新様式」を目指しただけでなく，新しくより良い一と確信していた一社会にふさわしい環境を持つ新世界を実現するというユートピア的目標を持っていたのである．

　このような未来への楽観的な信念は，たとえば1928年ストラスブールで完成されたテオ・ファン・ドゥースブルク，ゾフィー・トイバー＝アルプ，ジャン・アルプらの総合的な作品くオーベット〉の中にもはっきりと表現されているが，30年代になって回顧的でさらに反動的にさえなった時流の中でひどく冷遇された．それはスターリン体制下のソビエト連邦においてばかりか国家社会主義ドイツにおいても同様であった．1925−26年に工ル・リシツキーが構成主義の総合的な仕事としてハノーヴァー州立美術館に設置した抽象美術展示室（アブストラクテ・カビネット）がナチスの手によって1936年に破壊されたのはこういった動きの前兆であった．多くの国々で構成的美術の推進者たちは孤立を余儀なくされ，完全な沈黙を強いられる場合も多かった．彼らはすぐにちりぢりになった．その再編硬と強化の試みはパリでの1930年のミシェル・スーフォールの「円と正方形Cercle et Carr色」グループの結成と．1931年パリのオーギュスト・エルパンとジョールジュ・ファントンヘルローの「抽象＝創造Abstraction−Creation」グループの発足などの形に表われている．後者は幾何学的構成的美術の作家たちの世界的規模の連盟を作ることに成功した．定例展と定期刊行物を通し，活発なアイディアの交換をうながし，メンバーに国際的連帯感を与えた．パリではフランス語で言う「幾何学的抽象abstractiongeometrique」という表現形式を支持するこの運動は，当時支配的であった具象的，客観的絵画言語と夢や無意識から引き出された非現実的，幻想的な主題をもったシュルレアリスムに対する果敢な対抗運動であった．しかし，世界大戦を予告する暗雲がただよっていたパリでは，モンドリアンもカンディンスキーもそこに在住していたにもかかわらず，一般美術愛好者に支持されず，二人のどちらの作品もこのフランスの首都パリの公的コレクションには受け入れられなかった．「時代は陰鬱で，風向きは逆だった」とドイツの作家ベルトルトブレヒトは第二次世界大戦前とその最中の進歩的勢力の苦境を要約して述べている．

　構成的美術がその逆風を避けることができた好意的な土地も少しはあった．その一つはスイスであった．そこでは小グループの進歩的美術家が少数の不屈な精神のコレクターや美術館長の支援を受けて，構成主義とデ・ステイルの両方からの遺産を保持し，力つ更新しようとしていた．バーゼルやチューリヒで開かれた主要な構成的美術の展覧会は，創始者たちの想像力に富んだ成果を回顧させ，構成的美術を新たな話題として取り上げさせた．これと共に幾何学的，合理的技法の単純化がなされ，ある程度の規格化と客観化がなされた．1937年創立のアリアンツ（近代スイス芸術家連合）の中で最初にこの新絵画手法を体系的に応用したのは，マックス・ビル，カミーユ・グレーザー，リヒャルト・パウル・ローゼ，ヴエレーナ・レーヴエンスベルクなどのチューリヒに本拠を置く「具体美術」の代表作家らであった．中でもマックス・ビルは1949年執筆の重要な評論（「現代美術における数学的アプローチ」，1954年刊F美術と建築三　に所収）の中で，美術における数学的思考の重要性について注意を喚起した．ローゼも，同じ頃モジュールと連続の法則を発展させた．これは形体と色彩は同一であり，二つはもはや切り離せないとする美術の可能性を開いた．オランダのデ・ステイル運動やヨーロッパの構成主義と同じく，このグループも，美術家の仕事は象牙の塔にこもってする形式的，美的暇つぶしではなく，社会と文化の状況を変更しようとする実験的事業の一種であると見なしていたのである．マックス・ビルの画家，彫刻家，建築家，工業デザイナー，美術教師，展示デザイナー，理論家，はたまた政治家としての多様な活動はこうした態度の典型といえる．

　構成的美術は1945年になって，根本的変革を体験した後の∃一口ッパに再び現われた．運動自体もより強力になり，人間社会を国連憲章の路線に沿って再建し，改革さえしようとする意志を体現した有意義なものになった．狭い意味で美術界に限定すれば構成的運動は執拗に拡大していく主観主義に対抗する頑強な砦であった．主観主義は戦時中の個人の自由の束縛に対するごく自然の反動として50年代に盛んになった抽象表現主義．たとえば，タシスム，アンフォルメル，アメリカのアクション・ペインティングなどの傾向を生むこととなった．

　今やいたる所で視覚現象に関する研究が真剣に始められた．関心はさらに基本的な知覚作用にまで向けられた．チューリヒの「具体美術」の作家たちが行なった手法の体系化は，一部の地域では美術というより科学的な研究の一種に変化してしまった．構造の問題，連続の法則，知覚現象が，特に詳細に，体系的に研究された．「オブ・アート」としてその後知られるようになる錯視効果の美術がヴィクトール・ヴァザルリとブリジットうイリーにより提唱された．平面や色彩，レリーフ構造の動力学とか，光の運動効果，モビールなどのリアルな動き，空間を利用した作品など美術における「運動」を研究する地域的グループあるいは国際的グループが多くの国で形成された．モルレ，ソト，アガムらの「視覚芸術探究グループ」が，ヴァザルリと並んでパリで活躍したが，それは数多いキネティツク・アートのセンターのうちの一つにしか過ぎない．ドイツ，イタリア，ユーゴスラヴィア，ラテン・アメリカやソ連にすら同じようなグループが作られていた．（ウィリアム・C・サイツがこれらの傾向を概観する展覧会「応答する日」を1965年ニューヨーク近代美術館において行なった．）

　知覚現象と連続の法則およびプログラミングについての研究は，特にドイツとオランダにおいて情報美学の分野に進歩をもたらした．サイバネティクスに対する関′しが高まり，一定の法則の決定や，部分的修正などにコンピューターが使用されることもあった．偶然数またはランダム・ナノ′ヽ一無作為数に関心を持つ者がいて，それらの数は一定のシステムの中で沢山のデザインの中から実際に使うものを決定するのに利用された．こういったやり方については，1940年にすでにマックス・ビルが見通しを述べており，合理的で完全に制御された段階を踏んでの制作過程が，ある状況の下では合理的な説明が可能な境界線上に，あるいはその線上を越えた非合理の領域に達する結果になる場合があるのではないか，と言っている．

　ヨーロッパの構成的美術のさまざまな潮流がアメリカの美術家に与えた影響というのは，これまでごく限られたものに過ぎなかったし，今日でも事情は変わっていない．それでも1913年の伝説的なアーモリー・ショウ以来，進歩的な美術の発展に積極的に参加した個々のアメリカ人作家や美術愛好家は存在した．立体＝未来主義の技法の追求と，ダダイズムのあらゆる伝統的美術概念の否定との対照的な可能性が共に試みられた．マン・レイはアメリカ美術におけるこの新しい進歩的路線を推進した一人であった．また1920年頃マルセル・デュシャンの影響がパリよりニューヨークでより強かったのも偶然ではなかった．キヤスリーン・S・ドライアーとデュシャンが創立したソシ工テ・アノニム（株式会社）は，オランダのデ・ステイルやデッサウのバウハウス，さらにロシアにまで手をのばしてヨーロッパの先進的な美術家グループとの定期的な接触の機会をつくった．モンドリアンが提案し，1926年ブルックリン美術館で開かれたソシエテ・アノニムの近代国際美術展はそれらの仲介的活動の最高の成果であった．

　パトリック・ヘンリー・ブルース，アーサー・ダヴ，マースデンり＼一トレー，チャールズ・シーラー，ジョーゼフ・ステラ，マックス・ウェーバーなどほぼキュビスムを前提にして，そこから出発した新傾向の代表者たちに，まもなく1920年代の幾何学的抽象美術を推進したもっと若い世代がすぐに加わった．1927年ニューヨークのA・E・ガラティンによって創立された現代美術館（Museum of Living Art．1943年にフィラデルフィア美術館と合併）はモンドリアンの作品を中心とする構成的作品をアメリカ国内にもたらし，ガラティンが「非再現的」と名付けた美術を広めた．彫刻家ジョン・ストーズと画家ナイルズ・スペンサーも運動に加わった．1929年ニューヨークに近代美術館が創設され，現代美術の二大潮流一シュルレアリスムと構成主義−を知る最良の機会を提供した．あらゆる創造活動の分野を包括する新しい美術概念を広めようとしていた同美術館館長アルフレットH・バー・ジュニアは，パリ，デッサウのバウハウス，ソ連へと旅行し，強い刺戟を受けてさらに強力にその計画を推し進めようと決意した．1936年の「キュビスムと抽象美術」展は，アメリカ抽象美術家協会の創立と偶然重なって，丁度同じ頃にニューヨークのラインハート・ギャラリーで展覧会を開いていたジョージ・トK・モリス，ジョン＝フエレン，チャールズ・W・ショー，チャールズ・ピーダーマン，アレクザンダー・カルダーなど「具体主義者Concretionists」グループのような構成的美術家たちに新たな自信を与えた．それ以後，∃一口ッパやアメリカの幾何学的・構成的美術に属する作家の展覧会がニューヨーク市内外で頻繁に開かれるようになった．

　アメリカの美術家の多くは幾何学的アプローチを一時期体験してみるに過ぎなかったが，バーゴイン・デイラー，イリヤ・ボロトウスキー，チャールズ・ピーダーマン，ジョン・マクローリン，アレクサンダー・リーバーマン，フリッツ・ゲラーナーといったニューヨークに本拠を置く画家たちは，様式にははっきりとした違いがあったが，全員が構成的美術に対して貴重な貢献をした．ニューヨークで晩年を過ごし，そこで新境地を開きさえしたモンドリアンに対し少なからぬ崇敬の念が存在していたにもかかわらず，アメリカで構成的美術が認められたのは，かなり遅かった．

　しかし，アメリカを仕事場とした何人かのヨーロッパ作家の直接または潜在的な影響があったことを見落してはならない．たとえばシカゴで教鞭をとったラーズロ・モホリ＝ナシとか，ロシアの亡命者で非物質的なダイナミックな空間彫亥Ijのナウム・ガボ，〈正方形讃歌〉シリーズで倦むことなく「色彩の相関作用」を研究したジョーゼフ・アルバースなどである．このような色彩の法則とその効果に対する強い関心は，アドうインハートやマーク・ロスコらのように構成的美術の作家とは呼びにくい画家にまでおよんでいるのを見ることができる．そしてまた，彼らは，構成的精神を基礎とする「絵画的抽象以後post−painterlyAbstraction」の概念を発展させ続けている若い作家たちにも刺戟を与えた．フランク・ステラ，アル・ヘルド，ジョー・ベア，エルズワース・ケリー，ケネスリーランドらの画家や，ドナルド・ジャッド．カール・アンドレ，タン・フレイヴイン，ソル・ルウィット，フレッド・サンドバッグらの彫刻家一彼等のプライマリー・ストラクチュアズ（基本構造）の作品はミニマル・アートの領域に属する一は，ヨーロッパの若手の構成的美術家らによって，初めて取り上げられたのと同じ問題に取り組んでいる．

　1967年に構成主義の起源と展開について最初の総括的な書を著わしたのが，自身構成的で動く彫亥りを作るジョージ・リッキーというアメリカ人であったということは，ヨーロッパの立場から見て注目すべきことである．

　今日，「古典」となった構成主義は，いくつかの分派を持っている．プライマリー・ストラクチュアズの研究や，「芸術としての芸術ArtasArt」，「芸術についての芸術ArtaboutArt」のほかに，アグネス・マーティン，ジ工イク・バーソット，ジェイムズ・ビショップ，ロバート・ライマンらの作品に見られるような，最少限の線または色彩の変化の観察結果だけに自らを制限する「沈黙の芸術SilentArt」がある．ベルナール・ヴネの作品のようにコンセプチュアル・アートの流れには，その概念に目に見える形を与えるために構成的な法則を利用している例もある．ロバートマンゴールドが追求した単純な線の変化と乱れの作品も，この種の境界線上にある例である．

　構成的美術の作家たちは視覚と視覚創造の基礎的事実を実際に作品にもしたが，その中に含まれていた問題点は，以後，現在まで，60年以上にわたって繰り返し，さまざまの推論を生んだ．カンディンスキー，マレーヴィッチ，モンドリアン，ファン・ドゥースブルク，モホリ＝ナジから，クレー，アルバース，ローゼ，ビルおよびアメリカ人作家を含む現代の若い作家にいたるまで，構成的美術にはつきものの彼らの理論的な著述は，美術について語り得る事柄で最も啓示的なものを含んでいる．というのは，クレーの言った「絵画的思考」とは美術のみについての思考ではなく，結局はわれわれ人間と人間の住む世界についての思考であるからである．

（押原典子訳）